What Is The Enthalpy Change For This Reaction, In Kilojoules Per Mole Of Magnesium Reacting?
v.4: Enthalpy of Reaction
- Folio ID
- 21722
Learning Objectives
- To understand how enthalpy pertains to chemical reactions
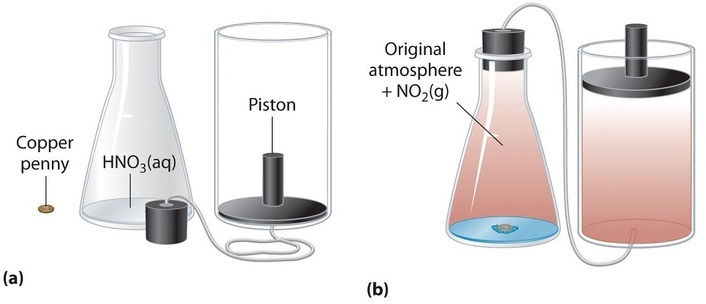
Nosotros have stated that the change in energy (\(ΔU\)) is equal to the sum of the heat produced and the work performed. Work done past an expanding gas is called force per unit area-volume work, (or just \(PV\) work ). Consider, for example, a reaction that produces a gas, such every bit dissolving a slice of copper in concentrated nitric acid. The chemical equation for this reaction is as follows:
\[ \ce{Cu(s) + 4HNO3(aq) \rightarrow Cu(NO3)ii(aq) + 2H_2O(l) + 2NO2(g)} \nonumber\]
If the reaction is carried out in a closed system that is maintained at constant pressure by a movable piston, the piston will rising equally nitrogen dioxide gas is formed (Figure \(\PageIndex{one}\)). The system is performing work by lifting the piston against the downward force exerted by the atmosphere (i.e., atmospheric pressure level). We find the corporeality of \(PV\) work done past multiplying the external pressure \(P\) by the change in volume caused by motility of the piston (\(ΔV\)). At a constant external pressure (here, atmospheric pressure level),
\[west = −PΔV \label{5.4.two}\]
The negative sign associated with \(PV\) work done indicates that the arrangement loses free energy when the volume increases. If the volume increases at constant pressure (\(ΔV > 0\)), the work done by the system is negative, indicating that a system has lost energy past performing work on its surroundings. Conversely, if the volume decreases (\(ΔV < 0\)), the work done by the arrangement is positive, which means that the environment have performed work on the organisation, thereby increasing its energy.
The internal energy \(U\) of a system is the sum of the kinetic energy and potential energy of all its components. It is the modify in internal energy that produces oestrus plus work. To mensurate the energy changes that occur in chemical reactions, chemists ordinarily apply a related thermodynamic quantity called enthalpy (\(H\)) (from the Greek enthalpein, meaning "to warm"). The enthalpy of a arrangement is defined as the sum of its internal free energy \(U\) plus the product of its force per unit area \(P\) and book \(V\):
\[H =U + PV \characterization{5.4.3}\]
Because internal free energy, force per unit area, and volume are all state functions, enthalpy is also a state function. And so we can define a change in enthalpy (\(\Delta H\)) accordingly
\[ΔH = H_{final} − H_{initial} \nonumber\]
If a chemic alter occurs at abiding pressure (i.e., for a given \(P\), \(ΔP = 0\)), the modify in enthalpy (\(ΔH\)) is
\[ \begin{align} ΔH &= Δ(U + PV) \\[4pt] &= ΔU + ΔPV \\[4pt] &= ΔU + PΔV \characterization{5.4.4} \finish{align} \]
Substituting \(q + due west\) for \(ΔU\) (First Constabulary of Thermodynamics) and \(−w\) for \(PΔV\) (Equation \(\ref{five.4.two}\)) into Equation \(\ref{v.four.iv}\), we obtain
\[ \begin{align} ΔH &= ΔU + PΔV \\[4pt] &= q_p + \cancel{westward} −\cancel{due west} \\[4pt] &= q_p \label{5.4.5} \end{marshal} \]
The subscript \(p\) is used here to emphasize that this equation is true merely for a process that occurs at constant pressure. From Equation \(\ref{5.4.v}\) nosotros see that at constant force per unit area the change in enthalpy, \(ΔH\) of the system, is equal to the heat gained or lost.
\[ \begin{align} ΔH &= H_{final} − H_{initial} \\[4pt] &= q_p \label{5.4.6} \end{align} \]
Just every bit with \(ΔU\), considering enthalpy is a land part, the magnitude of \(ΔH\) depends on merely the initial and final states of the system, not on the path taken. Most important, the enthalpy change is the same even if the process does not occur at constant pressure.
To find \(ΔH\) for a reaction, measure \(q_p\).
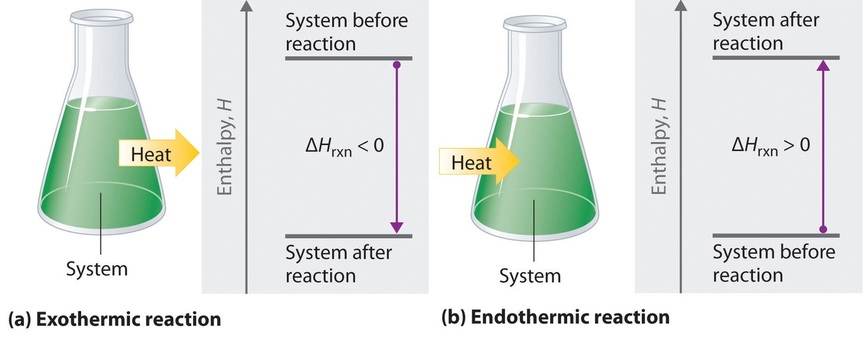
When nosotros study energy changes in chemical reactions, the almost of import quantity is ordinarily the enthalpy of reaction (\(ΔH_{rxn}\)), the alter in enthalpy that occurs during a reaction (such as the dissolution of a piece of copper in nitric acid). If oestrus flows from a system to its surroundings, the enthalpy of the system decreases, and then \(ΔH_{rxn}\) is negative. Conversely, if heat flows from the environs to a organisation, the enthalpy of the system increases, then \(ΔH_{rxn}\) is positive. Thus:
- \(ΔH_{rxn} < 0\) for an exothermic reaction, and
- \(ΔH_{rxn} > 0\) for an endothermic reaction.
In chemical reactions, bond breaking requires an input of energy and is therefore an endothermic process, whereas bond making releases energy, which is an exothermic process. The sign conventions for heat menstruum and enthalpy changes are summarized in the following table:
| Reaction Type | q | ΔHrxn |
|---|---|---|
| exothermic | < 0 | < 0 (heat flows from a arrangement to its environment) |
| endothermic | > 0 | > 0 (heat flows from the surroundings to a organization) |
If ΔH rxn is negative, and so the enthalpy of the products is less than the enthalpy of the reactants; that is, an exothermic reaction is energetically downhill (Figure \(\PageIndex{2}a\)). Conversely, if ΔH rxn is positive, then the enthalpy of the products is greater than the enthalpy of the reactants; thus, an endothermic reaction is energetically uphill (Effigy \(\PageIndex{2b}\)). Ii important characteristics of enthalpy and changes in enthalpy are summarized in the following discussion.
Bail breaking Always requires an input of energy; bail making ALWAYS releases energy.y.
- Reversing a reaction or a process changes the sign of Δ H . Water ice absorbs heat when it melts (electrostatic interactions are broken), so liquid water must release oestrus when it freezes (electrostatic interactions are formed):
\( \begin{matrix}
rut+ H_{2}O(s) \rightarrow H_{2}O(l) & \Delta H > 0
\end{matrix} \label{5.iv.seven} \)\( \begin{matrix}
H_{2}O(l) \rightarrow H_{two}O(s) + heat & \Delta H < 0
\cease{matrix} \label{five.4.8} \)In both cases, the magnitude of the enthalpy change is the same; just the sign is different.
- Enthalpy is an extensive holding (like mass). The magnitude of \(ΔH\) for a reaction is proportional to the amounts of the substances that react. For case, a large fire produces more heat than a single match, even though the chemic reaction—the combustion of wood—is the aforementioned in both cases. For this reason, the enthalpy alter for a reaction is normally given in kilojoules per mole of a particular reactant or production. Consider Equation \(\ref{5.4.9}\), which describes the reaction of aluminum with fe(III) oxide (Fe2Oiii) at constant pressure. According to the reaction stoichiometry, 2 mol of Iron, i mol of Al2O3, and 851.5 kJ of estrus are produced for every 2 mol of Al and 1 mol of Fe2Othree consumed:
\[ \ce{2Al(s) + Fe2O3(s) -> 2Fe (s) + Al2O3 (s) } + 815.v \; kJ \label{5.4.9} \]
Thus ΔH = −851.five kJ/mol of Fe2O3. We can also depict ΔH for the reaction as −425.eight kJ/mol of Al: because 2 mol of Al are consumed in the balanced chemic equation, we divide −851.5 kJ by 2. When a value for ΔH, in kilojoules rather than kilojoules per mole, is written afterward the reaction, every bit in Equation \(\ref{5.4.ten}\), it is the value of ΔH corresponding to the reaction of the molar quantities of reactants every bit given in the balanced chemical equation:
\[ \ce{ 2Al(s) + Fe2O3(s) -> 2Fe(southward) + Al2O3 (s)} \quad \Delta H_{rxn}= - 851.v \; kJ \label{v.4.ten} \]
If four mol of Al and 2 mol of \(\ce{Fe2O3}\) react, the change in enthalpy is ii × (−851.5 kJ) = −1703 kJ. We can summarize the human relationship betwixt the amount of each substance and the enthalpy change for this reaction every bit follows:
\[ - \dfrac{851.v \; kJ}{two \; mol \;Al} = - \dfrac{425.viii \; kJ}{ane \; mol \;Al} = - \dfrac{1703 \; kJ}{4 \; mol \; Al} \label{5.iv.6a} \]
The relationship between the magnitude of the enthalpy modify and the mass of reactants is illustrated in Example \(\PageIndex{1}\).
Instance \(\PageIndex{1}\): Melting Icebergs
Certain parts of the world, such equally southern California and Kingdom of saudi arabia, are brusque of freshwater for drinking. One possible solution to the problem is to tow icebergs from Antarctica and and so melt them as needed. If \(ΔH\) is half dozen.01 kJ/mol for the reaction at 0°C and abiding pressure:
\[\ce{Water(south) → H_2O(fifty)} \nonumber\]
How much energy would be required to melt a moderately large iceberg with a mass of ane.00 million metric tons (one.00 × ten6 metric tons)? (A metric ton is thousand kg.)
Given: free energy per mole of ice and mass of iceberg
Asked for: energy required to melt iceberg
Strategy:
- Calculate the number of moles of water ice contained in 1 meg metric tons (1.00 × 10half-dozen metric tons) of ice.
- Calculate the energy needed to melt the ice by multiplying the number of moles of water ice in the iceberg past the amount of energy required to cook ane mol of ice.
Solution:
A Because enthalpy is an extensive holding, the amount of free energy required to melt ice depends on the amount of ice present. We are given ΔH for the process—that is, the corporeality of energy needed to melt 1 mol (or eighteen.015 grand) of ice—and so we need to calculate the number of moles of ice in the iceberg and multiply that number past ΔH (+6.01 kJ/mol):
\[ \brainstorm{marshal*} moles \; H_{ii}O & = i.00\times 10^{6} \; \abolish{\text{metric ton }} \ce{H2O} \left ( \dfrac{1000 \; \abolish{kg}}{1 \; \cancel{\text{metric ton}}} \correct ) \left ( \dfrac{thou \; \abolish{1000}}{1 \; \cancel{kg}} \right ) \left ( \dfrac{1 \; mol \; H_{2}O}{18.015 \; \cancel{g \; H_{ii}O}} \right ) \\[4pt] & = 5.55\times 10^{10} \; mol \,\ce{H2O} \finish{marshal*} \]
B The energy needed to cook the iceberg is thus
\[ \left ( \dfrac{6.01 \; kJ}{\cancel{mol \; H_{2}O}} \correct )\left ( five.55 \times x^{ten} \; \cancel{mol \; H_{two}O} \correct )= three.34 \times 10^{11} \; kJ \nonumber \]
Because so much energy is needed to melt the iceberg, this plan would require a relatively inexpensive source of energy to be applied. To give you some thought of the calibration of such an performance, the amounts of different energy sources equivalent to the corporeality of energy needed to melt the iceberg are shown below.
Possible sources of the approximately \(3.34 \times 10^{11}\, kJ\) needed to cook a \(1.00 \times 10^6\) metric ton iceberg
- Combustion of 3.8 × ten3 ft3 of natural gas
- Combustion of 68,000 barrels of oil
- Combustion of 15,000 tons of coal
- \(1.1 \times 10^viii\) kilowatt-hours of electricity
Alternatively, nosotros can rely on ambient temperatures to slowly melt the iceberg. The master upshot with this idea is the cost of dragging the iceberg to the desired place.
Do \(\PageIndex{i}\): Thermite Reaction
If 17.3 g of powdered aluminum are allowed to react with excess \(\ce{Fe2O3}\), how much heat is produced?
- Answer
-
273 kJ
Enthalpies of Reaction
I way to report the estrus absorbed or released would be to compile a massive set of reference tables that list the enthalpy changes for all possible chemical reactions, which would crave an incredible amount of effort. Fortunately, since enthalpy is a state function, all nosotros have to know is the initial and last states of the reaction. This allows us to calculate the enthalpy change for virtually whatever conceivable chemical reaction using a relatively small ready of tabulated data, such as the following:
- Enthalpy of combustion (ΔHrummage) The change in enthalpy that occurs during a combustion reaction. Enthalpy changes take been measured for the combustion of virtually any substance that volition fire in oxygen; these values are unremarkably reported as the enthalpy of combustion per mole of substance.
- Enthalpy of fusion (ΔHfus) The enthalpy modify that acompanies the melting (fusion) of 1 mol of a substance. The enthalpy change that accompanies the melting, or fusion, of i mol of a substance; these values have been measured for almost all the elements and for most uncomplicated compounds.
- Enthalpy of vaporization (ΔHvap) The enthalpy change that accompanies the vaporization of 1 mol of a substance. The enthalpy change that accompanies the vaporization of one mol of a substance; these values have as well been measured for nearly all the elements and for most volatile compounds.
- Enthalpy of solution (ΔHsoln) The modify in enthalpy that occurs when a specified amount of solute dissolves in a given quantity of solvent. The enthalpy change when a specified amount of solute dissolves in a given quantity of solvent.
| Substance | ΔHvap (kJ/mol) | ΔHfus (kJ/mol) |
|---|---|---|
| argon (Ar) | vi.iii | 1.3 |
| methane (CH4) | 9.2 | 0.84 |
| ethanol (CH3CH2OH) | 39.three | vii.6 |
| benzene (C6H6) | 31.0 | 10.9 |
| h2o (H2O) | 40.vii | vi.0 |
| mercury (Hg) | 59.0 | 2.29 |
| iron (Atomic number 26) | 340 | 14 |
The sign convention is the same for all enthalpy changes: negative if heat is released by the system and positive if heat is captivated by the system.
Enthalpy of Reaction: https://youtu.be/z2KUaIEF9qI
Summary
For a chemical reaction, the enthalpy of reaction (\(ΔH_{rxn}\)) is the departure in enthalpy betwixt products and reactants; the units of \(ΔH_{rxn}\) are kilojoules per mole. Reversing a chemic reaction reverses the sign of \(ΔH_{rxn}\).
Source: https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_Chemistry_-_The_Central_Science_(Brown_et_al.)/05._Thermochemistry/5.4%3A_Enthalpy_of_Reaction
Posted by: rooksaddapprilk.blogspot.com


0 Response to "What Is The Enthalpy Change For This Reaction, In Kilojoules Per Mole Of Magnesium Reacting?"
Post a Comment